This page is a translation of the original work by Anu Dudhia that can be found at http://eodg.atm.ox.ac.uk/user/dudhia/rowing/physics/basics.html

 

Other recommended articles and pages
POE CURRENCY	BUY DIABLO 4 GOLD
BUY DIABLO 4 RUNES	BUY OSRS GOLD

 

Podstawy Fizyka Wiosłowania

(część org. pracy Fizyka Wiosłowania)

Spis Treści: Napęd Opór Energia kinetyczna Środek masy Warianty prędkości Równowaga Dźwignie Przekładnia dźwigni

 

1. Napęd

Łódź przyspiesza na zasadzie akcji i reakcji (trzecie prawo Newtona). Poruszasz wiosłem wodę w jedną stronę, łódź porusza się w drugą stronę. Pęd jako stosunek masy i prędkości oddziałujący "do wody" będzie równy i przeciwny do pędu otrzymanego przez łódź.

Wyobraź sobie łódź przed i po suwie.

Przed suwem całkowity pęd p = 0, ponieważ wszystko jest w stanie spoczynku.
Po suwie pęd całkowity: p = m_bv_b - m_wv_w = 0, ponieważ pęd całkowity nie może się zmienić (drugie prawo Newtona).

Na przykład, aby łódź z załogą m_b = 100 kg (t.j. jednoosobwa łódź) przyspieszyła ze stanu spoczynku do v_b = 1 m / s, musi mieć albo m_w = 10 kg wody i przyspieszyć do v_w = 10 m / s lub m_w = 20 kg wody do v_w = 5 m / s lub dowolna inna kombinacja m_w i v_w, która daje produkt mwvw = m_bv_b = 100 kg m / s.

Podczas normalnego suwu (tj. gdy łódź już się porusza) mniej oczywiste jest, że woda jest przemieszczana do tyłu, aby utrzymać łódź w ruchu do przodu, ponieważ pióra wydają się nie poruszać względem miejsca, w którym wchodzą do wody. Ale jeśli spojrzysz na taflę wody po wyjęciu piór widać, że woda się porusza. Aby przyspieszyć łódź, musi wystąpić jakiś spadek, jednak ze względów energetycznych (sekcja 3) powinień być jak najmniejszy.

A co jeśli odepchniesz się od dna rzeki lub szeregu słupków osadzonych wzdłuż brzegu zamiast wody? (Słyszę, że pytasz). Cóż, w takim przypadku cała planeta porusza się do tyłu i nadal występuje pewnien spadek(wykryty przez bardzo pedantycznego kosmonautę z nieprawdopodobnie precyzyjnym sprzętem pomiarowym).

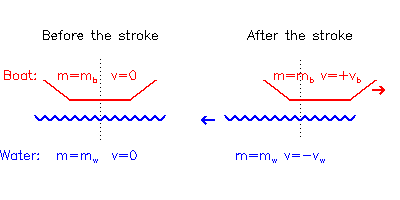
Rycina (1.1)

 

2. Opór

Ciała poruszające się w płynach zwalniają z powodu sił przeciwstawnych zwanych oporem. W rzeczywistości oznacza to przeniesienie pędu z ciała stałego do cieczy: otaczająca ciecz przyspiesza, gdy ciało stałe zwalnia, więc całkowity pęd pozostaje stały. W przypadku łodzi istnieją różne rodzaje oporu:

• Opór związany z tarciem wody o kadłub łodzi która przez nią płynie;
• Opór związany z turblencjami wywołanymi ruchem kadłuba;
• Opór falowy związany z utratą energi w wyniku tworzenia fal.

Łodzie wyścigowe są niezwykłe, ponieważ opór tarcia jest głównym źródłem oporu (około 80%). W większości innych łodzi dominuje opór falowy. Powietrze również przyczynia się do całkowitego oporu w podobny sposób (powietrze można traktować jako kolejną ciecz). Podczas gdy udział powietrza nieruchomego stanowi zaledwie kilka % oporu wody, prędkość powietrza jest znacznie bardziej zmienna, więc udział może wzrosnąć do 10% przy silnym wietrze.

Opór tarcia jest proporcjonalny do kwadratu prędkości, więc przy założeniu, że jego udział dominuje, całkowity opór R można zapisać jako

(2.1)

R = a.v2

gdzie v² jest kwadratem prędkości, a a jest stałą w zależności od powierzchni styku z wodąi kształtu kadłuba (będzie taka sama dla danej łodzi i tej samej załogi).

Aby utrzymać stałą prędkość, przykładana siła musi być równa oporowi R - nie było żadnego przyspieszenia ani opóźnienia (pierwsza zasada Newtona). Stąd średnia wymagana moc P (= siła x prędkość) wynosi:

(2.2)

P = a.v3

Oznacza to, że aby podwoić prędkość łodzi, musisz dostarczyć 2³ = 8 razy więcej siły. Innymi słowy, jeśli podwoisz siłe, przejdziesz tylko 1,26 (= 2^1/3) razy szybciej. Właśnie dlatego silne wiosłowanie nie pozwoli Ci tak szybko przegonić wioślarza, który wiosłuje lżej jakby Ci się wydawało. 

 

3. Energia kinetyczna

Korzystając z przykładu w sekcji 1, można osiągnąć określoną prędkość łodzi, niezależnie od tego, czy poruszałeś małą masę wody szybko, czy dużą masę wody powoli, o ile całkowity pęd pozostawał taki sam. Należy jednak wziąć pod uwagę całkowitą energię kinetyczną U (= ½ x masa x prędkość²) pozostałą w układzie po suwie

(3.1)

U = ½mbvb2 + ½mwvw2

Następnie dwa przykłady dają różne wyniki.
Jeżeli m_w = 10 kg i v_w = 10 m / s

 

(3.2)

U = 0,5 x 100 x 12+ 0,5 x 10 x 102 = 50 + 500 = 550 dżuli

ale jeśli m_w = 20 kg i v_w = 5 m / s,

(3.3)

U = 0,5 x 100 x 12 + 0,5 x 20 x 52 = 50 + 250 = 300 dżuli

Ta energia kinetyczna reprezentuje pracę mechaniczną wykonywaną przez wioślarza, ale w pierwszym przypadku musi wykonać prawie dwa razy większą pracę w celu osiągnięcia tej samej prędkości niż w drugim.

Aby osiągnąć określony wzrost prędkości łodzi, potrzeba mniej energii przy rozpędzaniu dużej ilości wody powoli niż małej ilości wody ale szybko. Jest to podstawowy argument przemawiający na korzyść dużych łyżek a także za to, żeby się nie opłukiwać.

 

4. Środek masy

Łódź w naszym przykładzie nie jest jednolitym ciałem stałym - zawiera trzy oddzielne elementy:

1. Załogę - stanowiąca 70–80% całkowitej masy;
2. Kadłub (i cox) - stanowiący 20–30% masy całkowitej;
3. Wiosła - stanowiące mniej niż 5% całej masy i w zostaną zignorowane.

Środek masy (CM) całego układu jest średnią ważoną masą pozycji CM każdego poszczególnego elementu. Podczas gdy poszczególne komponenty CM mogą poruszać się względem siebie, CM całego układu nie może zmienić swojego pędu (lub prędkości), chyba że zostaną przyłożone na nie siły zewnętrzne (zwykle przez wodę) (ponownie 1. prawo Newtona).

Jeśli załoga, masa m_c, siedzi nieruchomo w łodzi, masa m_b porusza się z prędkością v_t, to całkowity pęd układu wynosi m_cv_t + m_bv_t

Jeśli załoga zacznie następnie poruszać się rufowo z prędkością -v_c względem v_t, to łódź musi poruszać dziobem z inną prędkością względną v_b, aby zachować pęd:

(4.1)

mc vt + mbvt = mc (vt-vc) + mb (vt + vb)

co daje

(4.2)

mc vc = mb vb

 

Jeśli załoga stanowi 80% masy całkowitej (tj. m_c wynosi 4/5 m_c + m_b), to m_c = 4 m_b, więc v_b = 4 v_c. Jeśli załoga poruszy się na rufie przy prędkości v_c = 0,2 m / s, łódź poruszy się na dziobie o dodatkowe 0,8 m / s. W ciągu 1 sekundy wygląda z punktu widzenia załogi jakby przesunęli się o 1 m w kierunku rufy łodzi, ale dla osoby postronnej wygląda na to, że 80 cm z tego ruchu pokonała łódź w kierunku załogi.

Właśnie dlatego wydaje się, że łuki łodzi rwą po zakończeniu suwu: chociaż pióra wioseł zostały wyjęte i nie przyspieszają CM całego układu, ruch członków do tyłu w ich miejscach w łodzi przyspiesza kadłub do przodu w równym stopniu ale przeciwnym zwrocie. 

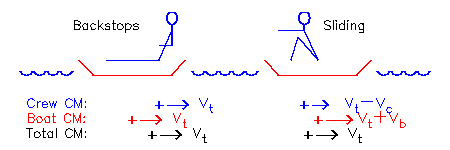
Rycina (4.1)

 

5. Warianty prędkości

Zależność mocy w zależności od prędkości (równanie 2.2) ma istotny wpływ na określenie mocy wymaganej do utrzymania średniej prędkości.

Jeśli załoga wiosłuje 1 minutę z prędkością 4 m / s, a następnie 1 minutę z prędkością 6 m / s, łączna odległość, którą pokonują, wynosi 60 x 4 + 60 x 6 = 600 m. Z równania (2.2), przy założeniu, że a = 1 kg / m dla uproszczenia równania, całkowita wymagana praca W (= siła x czas) wynosi

(5.1)

W = 60 x 43 + 60 x 63 = 16800 dżuli

a średnia moc w ciągu dwóch minut (= praca / czas) wynosi 140 Watów.

Załóżmy, że ta sama załoga wiosłuje tylko 2 minuty ze stałą prędkością 5 m / s. Pokonają taką samą odległość jak poprzednio, ale tym razem łączna wymagana energia jest inna

(5.2)

W = 60 x 53 + 60 x 53 = 15000 dżuli

więc średnia moc również jest zmniejszona i równa 125 watów. Zużyli więc średnio mniej mocy (lub mniej całkowitej energii) do pokonania tej samej odległości w tym samym czasie. Oznacza to, że bardziej energooszczędne jest utrzymywanie tego samego tempa podczas wyścigu niż, na przykład, startować szybko i następnie zwalniać lub startować powoli i przyspieszać.

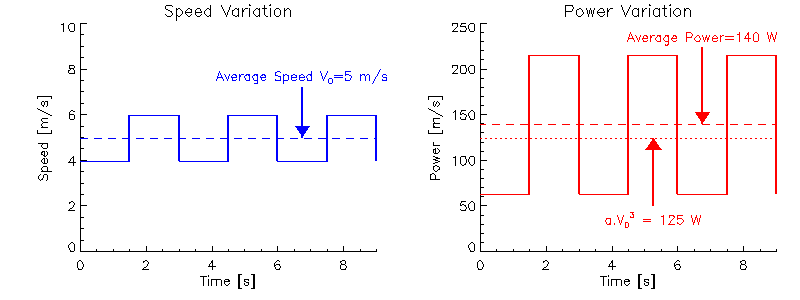
Rycina (5.1)

Ponieważ tarcie (równanie 2.1) zależy raczej od prędkości kadłuba niż prędkości całkowitego środka masy, te same argumenty dotyczą zmiany prędkości kadłuba podczas suwu (rysunek 5.1).

Jeśli kadłub spędza połowę każdego suwu z prędkością 4 m / s, a połowę z prędkością 6 m / s, jest mniej wydajny niż utrzymywanie stałej prędkości na poziomie 5 m / s (otrzymujesz dokładnie taką samą odpowiedź jak powyżej, jeśli podzielisz jednominutowy kawałek na 60 oddzielne 1 sekundowe elementy przeplatane 60 x 1 sekundowymi kawałkami z inną prędkością). Dlatego też niepożądane jest zbyt duże zróżnicowanie prędkości kadłuba podczas suwu (charakteryzujące się nadmiernym kiwaniem się dziobu lub rufy w górę i w dół).

W łodziach typu "sliding rigger" miejsce wioślarza jest w stałej pozycji, ale osadnice i podnóżek są połączone i mogą przesuwać się względem kadłubana łożyskach. Ponieważ wioślarz nie przesuwa się już w górę i w dół, zmiana prędkości kadłuba podczas suwu jest ograniczona, więc te łodzie są teoretycznie bardziej wydajne (tj. poruszają się szybciej przy takiej samej sile). Ponieważ te łodzie są obecnie zakazane, teoria przypuszczalnie działała, choć niekoniecznie tylko z powodu tarcia - opór falowy również jest mniejszy.

 

6. Równowaga

Łodzie pływają, ponieważ siła skierowana w dół spowodowana grawitacją jest równoważona siłą skierowaną w górę spowodowaną pławnością łodzi. Grawitacja działa tak, jakby masa całkowita była skoncentrowana w jednym punkcie, znanym jako środek masy lub środek ciężkości (CG). Siły wyporu działają również tak, jakby przyłożone w jednym punkcie, znanym jako środek wyporu (CB). CB pokrywa się z CG wypartego płynu, co nie jest tym samym punktem, co CG samego ciała pływającego

Gdy ciało stałe obraca się, CB porusza się względem kadłuba. Na przykład na ryc. 6.1, kiedy kadłub jest w pozycji pionowej, CB leży wzdłuż linii przerywanej, ale jeśli kadłub jest toczony w kierunku przeciwnym do ruchu wskazówek zegara (jak na rysunku), CB leży wzdłuż linii przerywanej. Przecięcie linii pionowych (sił wyporu) przez CB w różnych pozycjach przechylenia nazywa się metacentrum. Jeśli zanurzony kształt kadłuba ma okrągły przekrój (w cylindrycznym kadłubie), metacentrum (M) znajduje się po prostu w środku krzywizny.

Rycina (6.1)

To, czy ciało unosi się na wodzie nieruchomo czy ruchomo zależy od względnych pozycji metentrum i środka ciężkości.

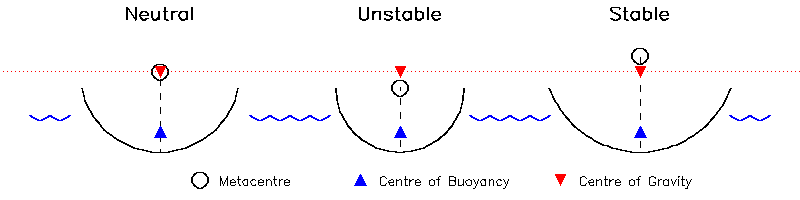
Lewy rysunek pokazuje przypadek, w którym M i CG pokrywają się. Pod dowolnym kątem przechyłu siła wyporu zawsze znajduje się bezpośrednio pod siłą grawitacji i moment skrętu nie występuje, dlatego będzie ona ustawiona pod dowolnym kątem w jakim się znajduje: będzie „neutralnie stabilny”. Przykładem tego jest pływający cylinder, w którym zarówno CG, jak i M pokrywają się z osią środkową.

Środkowa rycina ilustruje przypadek łodzi sportowej. Zanurzony kadłub jest prawie półkolisty (aby zminimalizować pole powierzchni: objętość styku z linią wody), stąd metacentrum leży blisko linii wodnej. Jednakże, aby osiągnąć skuteczny skok wioślarski, załoga musi usiąść kilka cali nad linią wodną, ​​więc CG (głównie załoga) leży powyżej M. Jeśli łódź toczy się w kierunku przeciwnym do ruchu wskazówek zegara, wyporność nadal działa w górę przez M, ale grawitacja działająca w dół w CG przesunęła się teraz w lewo, więc generowany jest moment obrotowy przeciwny do ruchu wskazówek zegara, który wzmacnia przechylenie - cały układ jest wewnętrznie niestabilny (jeśli nie wierzysz, wyjmij wiosła i zobacz jak długo będziesz w pozycji pionowej).

Prawa rycina pokazuje sytuację, w której CG znajduje się poniżej M, więc każde przechylenie w lewo powoduje, że CG porusza się w prawo względem M, aby wygenerować moment powrotu zgodny z ruchem wskazówek zegara, aby łódź była stabilna. Przykładem jest kajak z wioślarzem umieszczonym nisko w szerokim kadłubie łodzi.

Należy pamiętać, że stabilność jest określana tylko przez względne położenia środka ciężkości i metacentrum. Jest całkiem możliwe osiągnięcie stabilności dla wioślarza siedzącego nad linią wodną za pomocą kadłuba o płytszej krzywiźnie (podnosząc metacentrum do środka koła o większej średnicy - patrz ryc. 6.2). Właśnie dlatego łodzie treningowe są bardziej stabilne niż łodzie wyścigowe. Wadą jest zwiększenie pola powierzchni dla tego samego ułożenia, a zatem zwiększenie oporu.

Rycina (6.2)

Dlaczego więc łatwiej jest zrównoważyć poruszającą się łódź? Dwa powody:

1. Płetwa dużo lepiej tłumie przechylenia kiedy woda wokół niej przemieszca się;
2. Kształt łuków poruszających się w wodzie zwykle tworzy siłę stabilizującą.

Szczegółowe informacje można znaleźć w artykule Steve'a Kerra.

 

7. Dźwignie

Istnieją trzy klasy dźwigni w fizyce, wyróżniające się trzema możliwymi liniowymi pozycjami Punktu Podparcia, Ciężarem i Nacisk(Effort) (odpowiednio od lewej do prawej lub od prawej do lewej).

1. Ciężar - Punkt Podparcia - Nacisk
2. Punkt Podparcia - Ciężar - Nacisk
3. Punkt Podparcia - Nacisk - Ciężar

Ponieważ jedyną rzeczywistą różnicą między punktem podparcia i obciążeniem jest to, że punkt podparcia jest zdefiniowany jako punkt stacjonarny, różnica między dźwigniami klasy 1 i 2 zależy od twojego układu odniesienia (co trochę idzie w konflikcie z regulacjami FISA iż wiosła muszą stanowić dźwignie klasy 2).

Wiosło działa jak dźwignia, która w układzie odniesienia łodzi wygląda jak na ryc. (7.1) jako dźwignia klasy 1:

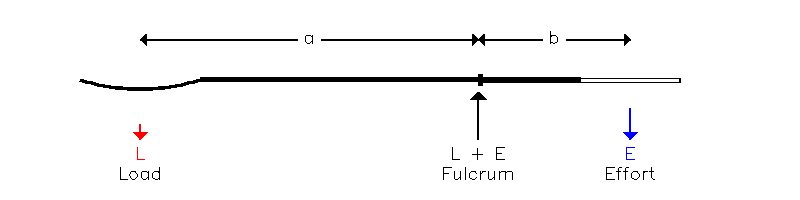
Rycina (7.1)

Strzałki pokazują siły działające na wiosło. Siły działające na łódź (na sworzniu i podnożku) są równe i przeciwne do sił na wiośle w punkcie podparcia i rączce, pozostawiając siłę wynikową L (w dół na rysunku). Siła napędowa przyłożona do wody jest równa i przeciwna do obciążenia łyżki, również L (do góry na rysunku). Stąd siły działające na łódź i wodę są równe i przeciwne.

Dla danego  E wartość obciążenia L jest określona przez stosunek długości b i a

(7.1)

L = E. (b / a)

Ponieważ dla zwykłego wiosła a jest większe niż b, siła występująca na piórze jest mniejsza niż siła przyłożona do rączki. Jeśli nie wydaje Ci się to prawidłowe, pamiętaj, że odległość przemieszczenia pióra jest odpowiednio większa niż odległość przesunięcia uchwytu, tak że Praca W wykonana na każdym końcu wiosła, zdefiniowana jako iloczyn (Siła x Odległość), pozostaje taki sam. Jeśli wiosło zostanie przesunięte o kąt y, odległość przesunięta przez uchwyt to b.y, a ostrze a.y, więc praca wykonana na każdym końcu wiosła wynosi:

(7.2)	uchwyt: W = E.b.y
(7.3)	pióro: W = L.a.y = E. (b / a) .a.y = E.b.y (przy użyciu 7.1)

Dla zewnętrznego obserwatora (np. urzędnika FISA stojącego na brzegu) sytuacja wygląda zupełnie inaczej - część stacjonarna (= punkt podparacia) wydaje się być piórem, a nie mocowania, dając następującą dźwignię klasy 2:

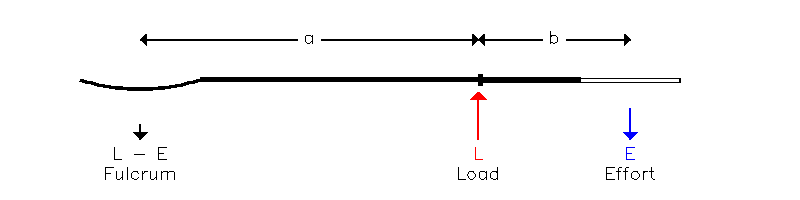
Rycina (7.2)

W tej konfiguracji obciążenie jest przykładane do sworznia i podawane przez stosunek długości a + b do długości a:

(7.4)

L = E. (a + b) / a = E + E. (b / a)

W tym przypadku wiosło zwiększa siłę przyłożoną do rączki. Należy jednak pamiętać, że siły i kierunki wzdłuż wiosła są takie same jak na ryc. (7.1) („punkt podparcia” i „ładunek” zostały po prostu ponownie oznakowane), tak że siły na łodzi i na wodzie również pozostają takie same. Jest to właściwie ogólna zasada:

Obliczone siły są takie same w dowolnym układzie odniesienia poruszającym się ze stałą prędkością.

Chociaż rama „stacjonarnego pióra” (ryc. (7.2)) jest lepsza z punktu widzenia trenera (np. uczenie wioślarzy, jak rozpędzadź łódź ponad końcem wiosła, zamiast przeciągając je przez wodę), ruchoma rama łodzi (ryc. (7.1)) oferuje łatwiejsze obliczenia matematyczne, więc wykorzystamy ją podczas omawiania przekładni dźwigni w następnej sekcji. W każdym razie odpowiedzi będą takie same.

 

8. Przekładnia dźwigni

Przekładnia dźwigni może być wyrażona po prostu jako stosunek odległości przemieszczonej przez Obciążenie do odległości przesuniętej przez Nacisk, który jest również taki sam, jak stosunek odległości Obciążenia i Nacisku w punkcie podparcia R (= (a / b)) (na ryc. 7.1). Ten stosunek R określa, jak „lekka” (mała R) lub „ciężka” (duża R) wydaje się woda przy różnych prędkościach łodzi.

Niestety Obciążenie i Nacisk wiosła nie są przykładane w ściśle określonych punktach, więc przekładnia jest tradycyjnie wyrażana w postaci długości, które można wygodnie zmierzyć.

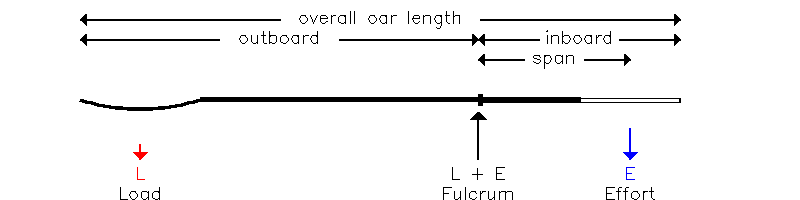
Rycina (8.1)

Odległość a jest zwykle przyjmowana jako długość wiosła zaburtowego (ryc. 8.1), mierzona od czubka pióra do zewnętrznej strony przycisku. Jednak to z kolei jest zazwyczaj wyrażane jako długość wewnętrzna (~ 115 cm), która jest łatwiejsza do zmierzenia, i całkowita długość (~ 375 cm), która jest (zwykle) stała (a ~ 375-115 = 260 cm).

Odległość b jest aproksymowana przez odstęp, zwany także rozpiętością lub TD („Thwartship Distance”), która dla łodzi z takielunkiem to odległość między środkiem sworznia a linią środkową łodzi (NB Rozpiętość dla wiosła definiuje się jako podwojenie tej odległości j. odległość między pinami). Zwróć uwagę, że b nie jest zdefiniowane przez długość wewnętrzną - zakłada się, że wioślarz skutecznie wywiera nacisk na wiosło powyżej linii środkowej łodzi, a nie na końcu rączki.

Aby zmienić rozpiętość, konieczne jest przesunięcie sworznia (łatwiejsza opcja) lub do środka (trudniejsza), a także powoduje to zmianę długości łuku w rzędzie. Szczegóły zależą od konstrukcji riggera i zwykle wymagają kilku porządnych sesji testowych.

Istnieje kilka metod zmiany przekładni dźwigni za pomocą odległości zaburtowych. Patrząc od metody najkrótszej do najdłuższej są to:

1. Umieszczenie „CLAMów” na zewnątrz przycisków. Efektywnie stanowią one dodatkowe przyciski zmniejszające odległość zaburtową o około 1 cm, a tym samym sprawiają że dźwignia jest lżejsza;
2. Przesunięcie samego przycisku w kierunku łyżki (dźwignia lżejsza) lub uchwytu (cięższa);
3. Zmiana długości wiosła. Przy utrzymaniu odległości burtowej na tym samym poziomie, wydłużenie wiosła spowoduje że dźwignia będzie "cięższa" a skrócenie "lżejsza".
4. Zmiana łyżki. "Tasaki" skuteczniej przekładają Nacisk bliżej końca niż wiosła typu "Macon", dlatego są zwykle o kilka cm krótsze, aby dać podobne odczucia przy tej samej odległości burtowej i rozpiętości.

Aby znaleźć równoważną zmianę da przy odległości zaburtowej a, która pozostawia przekładnię (a / b) niezmienioną po zmianie db dla odstępu b:

(8.1)	a / b = (a + da) / (b + db)
(8.2)	1 + db / b = 1 + da / a
(8.3)	da = (a / b) .db

Ponieważ a wynosi ~ 260 cm, b wynosi ~ 85 cm, (a / b) wynosi około 3, co jest zwykle określonym czynnikiem służącym do zrównania zmian rozpiętości ze zmianami pozycji przycisków. Na przykład zwiększenie rozpiętości o 1 cm powinno dać podobne odczucia jak zmiana pozycji przycisków o 3 cm.

 

---

Dodatek: Zasady Dynamiki Newton'a

1. Ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym jeżeli nie działa na nie żadna siła lub działające siły się równoważą
2. Zmiana przyspieszenia jest wprost proporcjonalna do działającej siły
3. Każda akcja wyłowuje reakcję o takiej samej sile i przeciwnym zwrocie